Programming in Arabesque

Arabesque simplifies the programming of Graph Mining Problems as presented in our paper. In the paper, we describe the system and provide a comprehensive introduction to the concepts that we describe below.

We show how Arabesque can be used to solve three fundamental problems in Graph Mining. Finding cliques, counting motifs and frequent subgraph mining. We chose these problems because they represent different classes of graph mining problems. Finding cliques is an example of dense subgraph mining, and allows one to prune the embeddings using local information. Counting motifs requires exhaustive graph exploration up to some maximum size. Frequent subgraph mining is an example of explore-and-prune problems, where only embeddings corresponding to a frequent pattern need to be further explored. We discuss these problems below in more detail.

Filter-Process Model: Think Like an Embedding

Our paper is the best introduction to the filter-process model, or "Think Like an Embedding" (TLE). We now summarize the TLE model, which is depicted below in its most basic form.

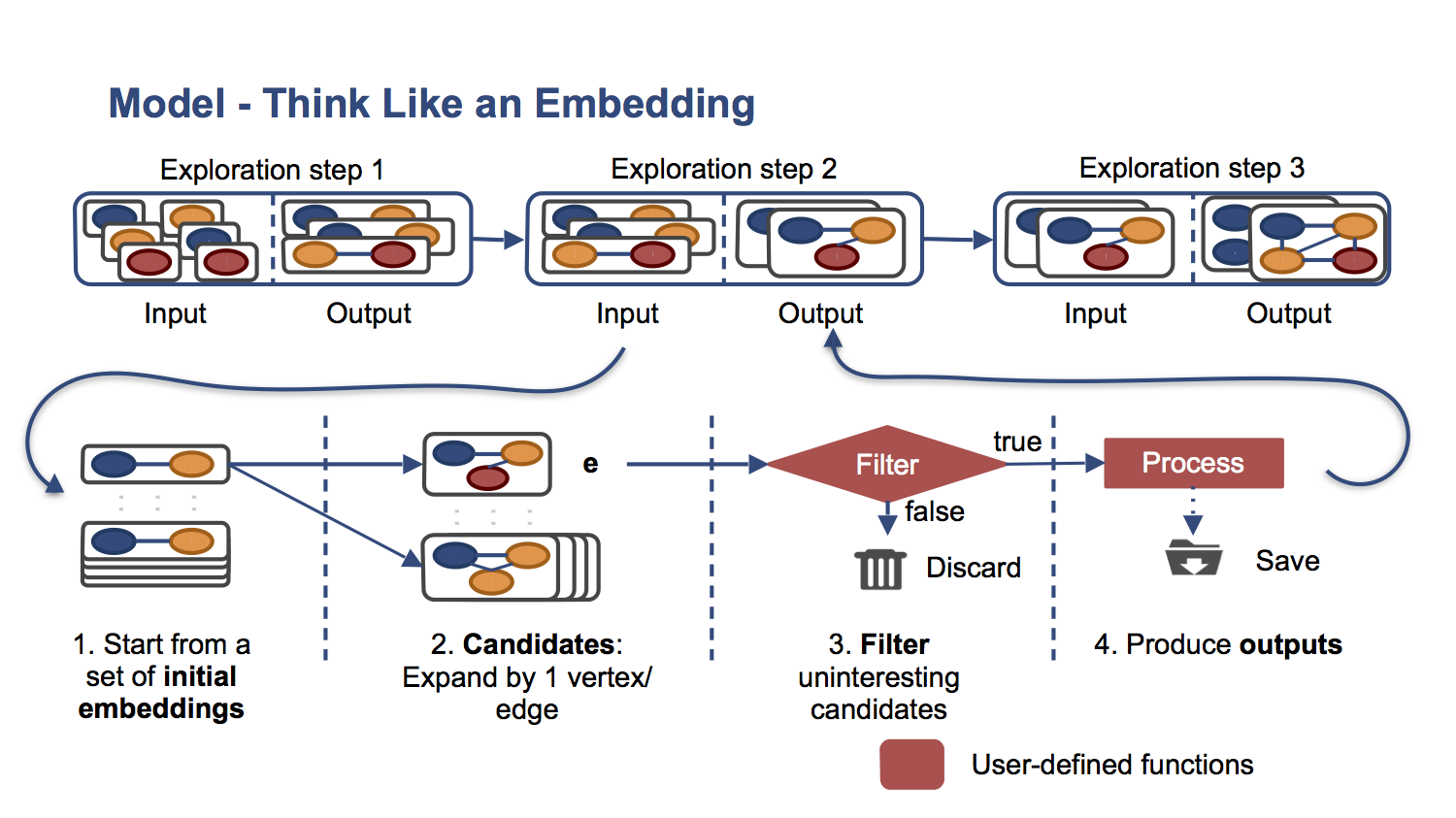
The systems exhaustively explores all subgraphs in the graph. We use the term embedding for a subgraph. Exploration proceeds in exploration steps. At each step the existing embeddings are expanded by one new neighboring vertex or incident edge, depending if the application wants vertex-based or edge-based exploration. If we add vertices, then every time a new vertex is added to an embedding, all the edges between the new vertex and the ones currently in the embedding are also added to the embedding, i.e., subgraphs are vertex-induced. If we add edges, then every time a new edge is added to an embedding, the vertex at the other end of the edge is also added (if it wasn't already in the embedding).

Each newly generated embedding, called candidate embedding, is streamed through a user-defined filter function, which returns a boolean saying whether the embedding is interesting or not. If the embedding is interesting, it is streamed over a user-defined process function, which typically derives some output from the embedding. After the process function, the new embedding is added to the set of embeddings to be expanded on the next exploration step. Before that, the embedding is streamed through an optional user-defined termination filter function, which is true by default and operates similarly to a filter function.

Applications that need to aggregate values across multiple embeddings can also define optional aggregation functions. Their operation is depicted below:

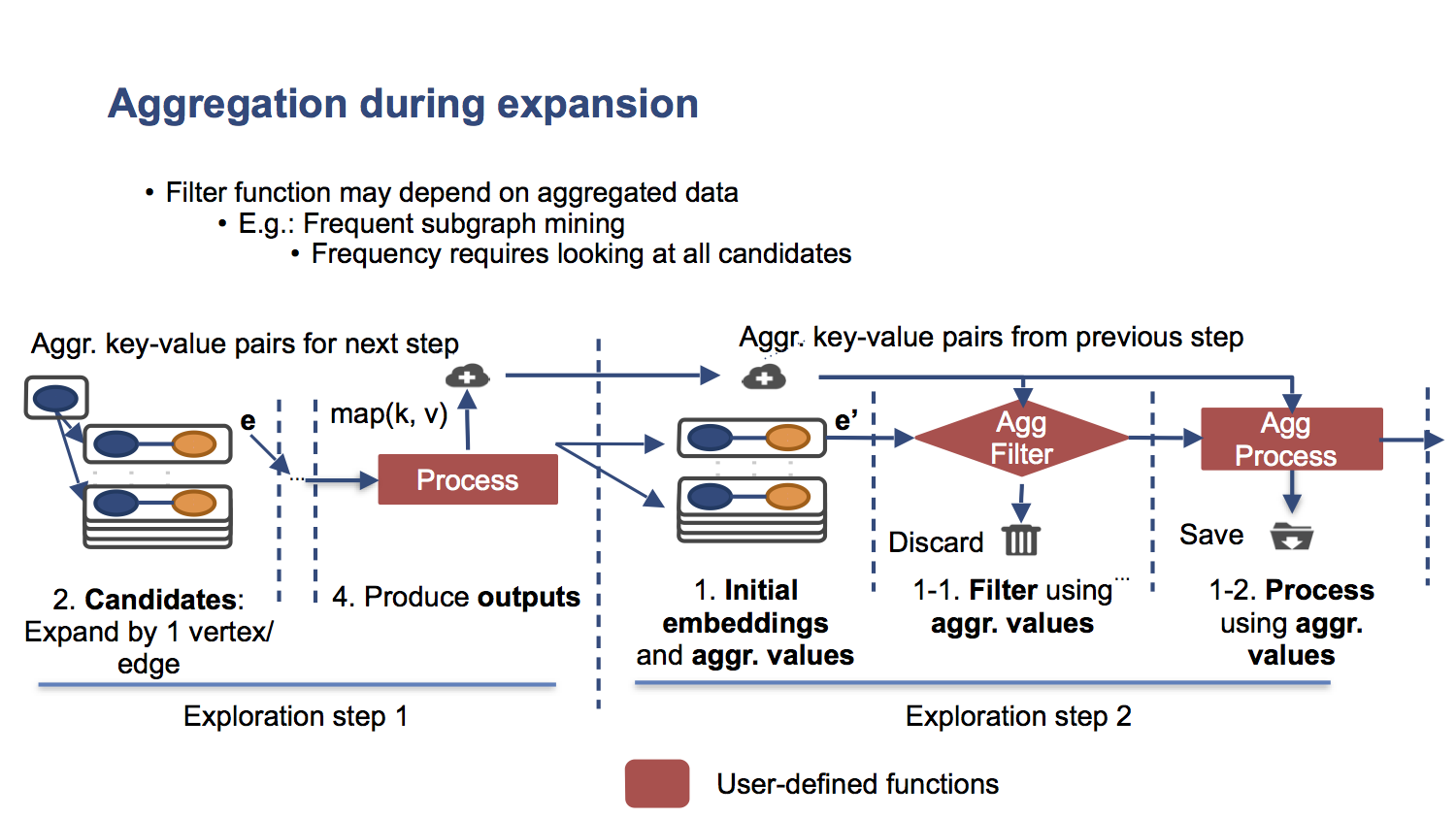
The process function can call a map function, which sends a key-value pair (k, v) to a certain aggregator. This aggregator then runs a user-defined reduce function to merge all (k, v) pairs with the same key k. The aggregated values become available for reads by user-defined functions at the end of the exploration step. Before the filter function, Arabesque executes two user-defined functions that can take advantage of aggregated values: aggregate-filter and aggregate-process, which are analogous to the filter and process function. These two additional functions allow pre-filtering and pre-processing based on values aggregated in the previous steps.

Arabesque API

Let us see how to create a new computation in Arabesque. Arabesque operates in two modes: vertex-induced and edge-induced expansion. For algorithms using vertex-induced expansion, it is necessary to create a new class that extends VertexInducedComputation; for algorithms using edge-induced expansion, the new class must extend EdgeInducedComputation. Implementing a computation entails overriding methods of the parent class. Both parent classes extend the following interface (we report only the most important methods).

public interface Computation<E extends Embedding> {
     void init();

     boolean filter(E embedding);

     void process(E embedding);

     boolean shouldExpand(E newEmbedding);

     void initAggregations();

     boolean aggregationFilter(E Embedding);

     void aggregationProcess(E embedding);
 }

The class E can be either VertexInducedEmbedding or EdgeInducedEmbedding, depending on the type of computation we are using.

Computation classes can have a local state, which will be replicated at each Arabesque worker thread running the job. The init method initializes this internal state (it must start with a call to super.init()). The filter method executes the filter function and the process method executes the process function. Finally, the method shouldExpand implements the termination filter function. These methods are sufficient to implement the basic filter-process model.

Algorithms using aggregation can also override the aggregation filter and aggregation process functions. In order to use aggregations, applications need to register them by specifying the key and value classes, as well as the reduction function. This must be done in the initAggregations method, which typically looks like the following example.

@Override
public void initAggregations() {
    super.initAggregations();

    Configuration conf = Configuration.get();

    conf.registerAggregation(
        "my-aggregation", // Aggregation name
        KeyClass.class, // The class of key objects
        ValueClass.class, // The class of value objects
        false, // Is this aggregation persistent (i.e  an output aggregation)
        new ReductionFunctionImplementation() // This specifies the reduction function to use.
    );
}

The method registerAggregation takes as input the specification of the reducer of an aggregation. Arabesque supports using multiple aggregations. Each aggregation is associated with a unique name (a String), has multiple keys, and is processes independently from the others. In the example, the aggregation is called "my-aggregation". The following two arguments are the classes of keys and values, respectively, which must implement the Writable interface. The third argument is a boolean with value true if the aggregated values are persisted until the end of the computation (in this case we talk about an output aggregator); a value false indicates that values are recomputed anew at each exploration step. Finally, the last argument indicates the user-defined class implementing the reducer logic. This class must implement the following simple interface, to aggregate two values into one:

public interface ReductionFunction<V extends Writable> {
    V reduce(V k1, V k2);
}

Applications can map values to a reducer by invoking the void map(String name, K key, V value) method and read aggregated values using AggregationStorage<K, V> readAggregation(String name).

Application Examples

We now show implementation examples for three applications: finding cliques, counting motifs, and frequent subgraph mining.

Finding Cliques

Finding cliques has many variations. Here, we present the variation of finding cliques of a maximum size. Following, we have the implementation in Arabesque:

public class CliqueComputation 
        extends VertexInducedComputation<VertexInducedEmbedding> {
    private static final String MAXSIZE = "arabesque.clique.maxsize";
    private static final int MAXSIZE_DEFAULT = 4;

    int maxsize;

    @Override
    public void init() {
        super.init();
        maxsize = Configuration.get().getInteger(MAXSIZE, MAXSIZE_DEFAULT);
    }

    @Override
    public boolean filter(VertexInducedEmbedding embedding) {
        return isClique(embedding);
    }

    private boolean isClique(VertexInducedEmbedding embedding) {
        return embedding.getNumEdgesAddedWithExpansion() 
                == embedding.getNumVertices() - 1;
    }

    @Override
    public void process(VertexInducedEmbedding embedding) {
        if (embedding.getNumWords() == maxsize) {
            output(embedding);
        }
    }

    @Override
    public boolean shouldExpand(VertexInducedEmbedding newEmbedding) {
        return newEmbedding.getNumWords() < maxsize;
    }

}

In Arabesque, the user must define the Computation class for the problem at hand. In this particular case, we have defined the class CliqueComputation that extends the VertexInducedComputation, which dictates that the exploration Arabesque will perform is vertex-induced. As we explained before, this exploration extends an embedding by connecting it to a new vertex at a time. All edges connecting that new vertex to existing vertices of the embedding are also added.

To solve the problem and control the exploration the user defines two main functions. The filter function decides whether the passed embedding is a valid clique and, thus, if it should be further expanded and processed. The process function dictates what to do with the embeddings that passed the filter function. In this particular problem, we only want to output the embeddings. Note, that the complexity of the exploration and the required checks for avoiding redudant work, and the canonicality checks are completely transparent to the end-user. This filter function trivially respects the anti-monotonicity property as if a parent is not a clique, there's no chance for any of its children to be cliques.

For performance reasons, the filter is implemented in an incremental way. The current embedding was constructed by extending a parent embedding with some new vertex and all the edges that connect it to existing vertices in the embedding. Thus we can efficiently implement the filter function by only considering whether the vertex we added connects to all previous vertices in the parent embedding. This can be done very easily, by getting the number of new edges added to this embedding getNumEdgesAddedWithExpansion() and checking if this number is equal to the number of vertices in the parent embedding which by default is one less than the current embedding.

To produce the output, we simply check whether we have reached the size of cliques we are interested in. The output function saves that embedding to HDFS.

To avoid going to deeper depths than the one we want to discover, the user can override the optional shouldExpand function that checks whether we need to further expand the embedding and thus continue the exploration. By default, this function returns true, and by overriding it we can stop the processing faster.

Counting Motifs

A motif is defined as a connected pattern of vertex induced embeddings that exists in an input graph. Further, a set of motifs is required to be non-isomorphic, i.e., there should obviously be no duplicate patterns. In motif mining there is no minimum frequency threshold; rather the goal is to extract all motifs that occur in the graph along with their frequency distribution. Since this task is inherently exponential, motifs are typically restricted to patterns of order (i.e., number of vertices) at most k. For example, for k = 3 we have two possible motifs: a chain where ends are not connected and a (complete) triangle. Following, we have the Motif counting implementation in Arabesque:

public class MotifComputation 
        extends VertexInducedComputation<VertexInducedEmbedding> {
    private static final String AGG_OUTPUT = " output";
    private static final String MAXSIZE = "arabesque.motif.maxsize";
    private static final int MAXSIZE_DEFAULT = 4;

    private static LongWritable reusableLongWritableUnit = new LongWritable(1);
    private int maxsize;

    @Override
    public void init() {
        super.init();
        maxsize = Configuration.get().getInteger(MAXSIZE, MAXSIZE_DEFAULT);
    }

    @Override
    public void initAggregations() {
        super.initAggregations();

        Configuration conf = Configuration.get();

        conf.registerAggregation(
            AGG_OUTPUT,
            conf.getPatternClass(), 
            LongWritable.class, 
            true,
            new LongSumReduction()
        );
    }

    @Override
    public void process(VertexInducedEmbedding embedding) {
        if (embedding.getNumWords() == maxsize) {
            map(AGG_OUTPUT, embedding.getPattern(), reusableLongWritableUnit);
        }
    }

    @Override
    public boolean shouldExpand(VertexInducedEmbedding newEmbedding) {
        return newEmbedding.getNumWords() < maxsize;
    }
}

The Computation class, MotifComputation, extends the VertexInducedComputation, which dictates that the exploration that Arabesque will perform is Vertex Induced in a similar way to finding cliques.

For counting Motifs, we are interested in all possible variations of the embeddings and thus we don't need to implement a special filter function. The default filter function returns true and is sufficient for this problem. For the process implementation, we need to compute for every embedding the pattern it corresponds to (motif for this problem), and then group it over all embeddings to compute the frequencies of the motifs. In Arabesque, this is performed through the user of aggregations, which work similarly to Giraph's Aggregators, and allow one to compute aggregate statistics on a pattern level or any other arbitrary key. In the process function, we simply generate a new unit key-pair containing the pattern that this embedding corresponds to as the key and 1 as the value. To be able to use an aggregation, we first need to initialize it. This is done in the initAggregations function. Here, we define the key and value types as well as how to reduce values belonging to the same key. For motifs, a simple sum reduction is sufficient.

The shouldExpand behaves identically to the Finding Cliques computation, terminating the expansion when the desired depth has been reached.

Frequent Subgraph Mining

Frequent subgraph mining (FSM) focuses on finding patterns whose frequency in the input graph is above a certain threshold. The FSM task outputs all frequent patterns and their respective embeddings (i.e., matching subgraphs) from a single input graph.

In our implementation, frequency is counted using an anti-monotonic metric called "Minimum Image-Based" (MNI) support (see B. Bringmann and S. Nijssen. "What is frequent in a single graph?" PAKDD 2008). We chose this metric because it is anti-monotonic. By contrast, simply counting the number of subgraphs that match a pattern is not an anti-monotonic frequency metric. According to such metric, the expansion of an infrequent pattern may be frequent. We refer the reader to our SOSP paper for a precise description of the MNI metric.

In frequent subgraph mining, we use aggregation to calculate the frequency/support of each pattern we see. The frequency/support metric is based on the notion of domain, which is defined as the set of distinct mappings between a vertex in a pattern and the matching vertices in any automorphism of an embedding. The process function maps the domains of an embedding to its respective pattern. The DomainSupportReducer function merges 2 domains into one by merging all internal mappings for each vertex position. Note that in this example, we use one more parameter when registering the aggregation. This is called an end aggregation method, which is invoked every time aggregation completes. This method is useful for cases where we have a very large number of keys, as it happens with FSM. Finalized aggregated values, in fact, are broadcasted to all workers in the system. End aggregation methods can be used to eliminate keys whose value is useless and that do not need to be further use, and therefore broadcasted. In this example, the DomainSupportEndAggregationFunction function will look at all aggregated (Pattern, DomainSupport) pairs and only keep those where the DomainSupport is above a predetermined threshold. This is a performance optimization to prevent having to broadcast a large amount of pairs that are of no value to us because we already know they are not frequent. The aggregationFilter function then consults the surviving key-value mapping to see if the pattern of the current embedding is contained in that mapping. If it is, that pattern is frequent so the current embedding should be processed. This is then done via the aggregationProcess function which outputs all embeddings that survive the aggregation-filter.

public class FSMComputation 
        extends EdgeInducedComputation<EdgeInducedEmbedding> {
    public static final String AGG_SUPPORT = "support";

    public static final String CONF_SUPPORT = "arabesque.fsm.support";
    public static final int CONF_SUPPORT_DEFAULT = 1000;

    public static final String CONF_MAXSIZE = "arabesque.fsm.maxsize";
    public static final int CONF_MAXSIZE_DEFAULT = -1;

    private DomainSupport reusableDomainSupport;

    private AggregationStorage<Pattern, DomainSupport> previousStepAggregation;

    private int maxSize;
    private int support;

    @Override
    public void init() {
        super.init();

        Configuration conf = Configuration.get();

        support = conf.getInteger(CONF_SUPPORT, CONF_SUPPORT_DEFAULT);
        maxSize = conf.getInteger(CONF_MAXSIZE, CONF_MAXSIZE_DEFAULT);

        reusableDomainSupport = new DomainSupport(support);

        previousStepAggregation = readAggregation(AGG_SUPPORT);
    }

    @Override
    public void initAggregations() {
        super.initAggregations();

        Configuration conf = Configuration.get();

        conf.registerAggregation(
            AGG_SUPPORT,
            conf.getPatternClass(), 
            DomainSupport.class,
            false,
            new DomainSupportReducer(), 
            new DomainSupportEndAggregationFunction()
        );
    }

    // Previous Step embeddings
    @Override
    public boolean aggregationFilter(EdgeInducedEmbedding previousStepEmbedding) {
        // Using the DomainSupportEndAggregationFunction, we 
        // removed all mappings for non-frequent patterns. 
        // So we simply have to check if the mapping has
        // the pattern for the corresponding key
        return previousStepAggregation.containsKey(previousStepEmbedding.getPattern());
    }

    @Override
    public void aggregationProcess(EdgeInducedEmbedding previousStepEmbedding) {
        output(previousStepEmbedding);
    }

    // Current step embeddings 
    @Override
    public void process(EdgeInducedEmbedding embedding) {
        reusableDomainSupport.setFromEmbedding(embedding);
        map(AGG_SUPPORT, embedding.getPattern(), reusableDomainSupport);
    }

    @Override
    public boolean shouldExpand(EdgeInducedEmbedding newEmbedding) {
        return maxSize < 0 || newEmbedding.getNumWords() < maxSize;
    }
}

The Computation class FSMComputation extends the EdgeInducedComputation class, which determines that the exploration is edge induced, a different exploration strategy to the previous two Applications. Similar to Motifs, no filter function is defined. The reasoning for such an omission, however, is different than in the case of Motifs. With FSM we cannot filter based on the information of a single subgraph alone and need to wait until the aggregated frequency values are ready to then filter the embeddings with the aggregationFilter function.

To obtain the aggregated frequencies, we use a non persistent aggregation. These behave in a similar manner to output aggregations with the difference that their values do not persist until the end of the execution. That is, at each different step, the content of interstep aggregators are reset.

The process function for FSM is responsible for creating the key-value pairs that, when aggregated, will result in (Pattern, DomainSupport) from which we can extract the set of frequent patterns.

Similar to the other algorithms, the user can define the optional shouldExpand function to prune explorations of very big subgraphs.

The FSM algorithm also contains an optional MasterComputation. This MasterComputation is called after the end of a superstep and allows you complete access to the values of the aggregations before the start of the next step. In this example, we use this access to output the frequent patterns that we see at each step as well as to terminate execution earlier if we immediately detect that there are no frequent patterns (and, therefore, all aggregationFilter calls will return false at the next step).

public class FSMMasterComputation extends MasterComputation {
    @Override
    public void compute() {
        AggregationStorage<Pattern, DomainSupport> aggregationStorage = 
            readAggregation(FSMComputation.AGG_SUPPORT);

        if (aggregationStorage.getNumberMappings() > 0) {
            System.out.println("Frequent patterns:");

            int i = 1;
            for (Pattern pattern : aggregationStorage.getKeys()) {
                System.out.println(i + ": " + pattern);
                ++i;
            }
        }
        // If frequent patterns is empty and superstep > 0, halt
        else if (getStep() > 0) {
            haltComputation();
        }
    }
}

Developing your own algorithms

The easiest way to start developing your own graph mining algorithms on top of Arabesque is to clone our Arabesque-Skeleton repository. This gives you a preconfigured Maven project with detailed instructions on how to get your code running in a cluster.